特別支援教育
磐田市で3年間、幼児の就学支援の業務に携わった。園での様子を見に行ったり、保護者と面談を行ったりした。資料を作成して市や県の就学支援委員会の審議を行い、小学校入学時に特別支援学校や特別支援学級などにつなぐお手伝いをしてきた。公私立園だけでなく、認可外の園も含め、年間100件近くの幼児にかかわり、自分なりに分かってきたことがある。
園の保育者は、良かれと思ってその子を療育に通わせようとするが、小学校入学後のその子の姿が意外と見えていない。
小学校教員は、良かれと思ってその子を特別支援学級などに入れようとするが、中学校卒業後のその子の社会自立が意外と見えていない。
その結果、園でも小学校でも、「就学支援」が、通常学級に居られない大変な子の選別作業になりかねない。そのための手段として、知能発達検査や医療受診を勧めることになる。
磐田市就学支援委員会では、義務教育の期間に審議する児童生徒数と、園の年長児の審議数がほぼ同じだった。小学校入学時にかなりの数の、特別支援学校や特別支援学級の判断を出しているのである。
不思議なのは、園では何ともなかった、または、何とかやれていた子が、小学校入学後に就学支援の対象児となることである。小学校の特別支援コーディネーターから園に、「何で情報をあげてこなかったのか」と言われ、困惑することになる。別に隠していたわけではなく、園では問題はなかったのである。そんな事例が、年に数件あった。小1ギャップといわれるものの何割かは、小学校による環境調整の失敗ではないかと、私は思う。責任を園や保護者に求められても困るのではないだろうか。
「インクルーシブ教育」として、意識したいことが3点ある。本校の職員にも伝えていくつもりである。
・障害の有無に関係なく、すべての子が幸せに学校生活を過ごすための環境調整である。
・診断名や検査結果だけで子どもを判断せず、成育歴や愛着の形成歴に思いを寄せる。
・今、その子をどうするかだけでなく、その子の社会自立までを視野に入れて支援する。
その他
みなさんは「おおきなかぶ」の話を知っていますね。1年生の国語の教科書にも載っています。どんなお話だったか思い出してください。おじいさんとおばあさんと孫の3人で引っ張ってもぬけないとき、どうしましたか。孫は犬をよんできました。どうせなら力持ちの大人かジャイアンを連れてくればよかったのに、なぜ、犬だったのでしょう。
校長先生は、「大きなかぶ」のお話には秘密があると思うのです。犬は孫を引っ張るだけでなく、かぶの周りの土を掘ったのかもしれません。犬はだれをよびましたか? 仲間の大きな犬ではなく、自分より小さいねこでした。犬とねこで、かぶの周りの土をほり、ぬけやすくし、その間に人間は休めたかもしれません。ねこはだれをよびましたか? 大きなねこではなく自分よりも小さいねずみです。ねずみは、力も弱いし、あなをほるのもとくいではありません。でも、じょうぶな歯でかじることができます。大きなかぶの先っぽの根っこをかみ切ってぬけやすくしたかもしれません。ねこが苦手なはずのねずみが、ねこといっしょにひっぱったところもすごいです。
なにより、かぶがぬけないときに、犬をよんできた孫のアイデアはすごいと思います。みんなも、何かうまくいかないときに、あたりまえのことをしてもダメなことがあるでしょう。新しい時代をつくっていく人は、あきらめずにいろいろなアイデアを試せる人なのです。アマゾンやアップル、フェイスブックなどの世界的に有名な会社を作った人たちは、子どものころは、勉強は苦手で、ちょっと変わったところがあったそうです。でも、大人になって大成功しました。
今は、いろいろな考え方や感じ方をもった人が、おたがいの良さを認め合うことが大切な時代です。犬をよんできた女の子に「お前何やってんの。犬なんか呼んでも役に立つわけないじゃん。」と言うようでは、よい世界になっていかないと思います。
みんなでひっぱって、かぶがぬけたというだけのお話ですが、いろいろと考えながら読むと、役に立つことが書かれていると思います。みんなが持っている力やよいところを出し合って1つのことをなしとげるということは、大人になっても役立ちます。あなたのいいところと、友達のいいところを合体させて、笠原小学校をすてきな学校にしていきましょう。
【原稿に追加】 ところで、大きなかぶをどうやって食べたと思いますか。寒い土地であるロシアの昔話ですから、かぶは、5年生が今日学習していた「てんさい」のことです。しぼって砂糖を作ったと思います。だから、おじいさんは、「あまいあまいかぶになれ」と言っていたでしょう。おおきなかぶは、おおきなてんさいなのです。
(6月21日 第2回会礼 校長の話)
子どもたちに「インクルーシブ」の考えを伝えたくてこのような話をしました。前回の「ももたろう」に続き、昔話+ジャイアンが鉄板ネタになってきました。

特別支援教育
前の職場では、給食がなかったので、週に1~3回は、近くの店で外食をしていました。安くてボリュームがあって、しかもおいしいので店はいつも混んでいました。揚げ物がメインの「か〇や」というひらがな3文字のお店です。(まん中の字はあえてふせておきます)
レジの奥の壁には、店是のプレートがかかっていて、こう書かれていました。「店はお客のためにある」
何を当たり前のことを今さら・・・・、と思いながら、深い意味でもあるのかと調べてみると、倉本長治の商訓五十抄の言葉だと分かりました。「店は客のためにあり 店員とともに栄える」というのが元の言葉です。
学校現場に戻ってきて、そもそも学校は何のためにあるのかと考えてみると、この言葉の大切さが身に沁みます。
学校は子どものためにあり、教員とともに伸びていく場所であるべきだと思い至りました。そんな学校をつくるためには、「インクルーシブ」の共通理解が必要だと思うのです。
子どものために教育環境を変えたり整えたりするのは、特別扱いではありません。手が掛かる子に対して、「わがまま」「自分勝手」「親からの愛情不足」と決めつけ、子どもや親が変わるべきだと思っている教員がいるとしたら、危険です。また、同僚に対して「あなたの指導が甘いから、学級が荒れる」「やるべきことはきちんとやらせなければダメ」と助言する教員も同じく危険です。
不寛容と排除の論理で、特別支援学級に入る子と不登校の子が増え続ける今の小中学校のシステムは、何か間違っているのではないでしょうか。「何もかもしっかりできないと通常学級にいてはいけない」という息苦しさを、敏感な子どもたちが感じている状態なのだと思います。
学校は子どものためにあるのですから、変わるべきは「そろえたい」「やらせたい」教員の方なのです。それが、「インクルーシブ」共通理解のスタートです。インクルーシブ教育は、特別支援教育の亜種ではありません。
教員の考えや行動が変わることで、子どもも変わると、私は信じています。「笠原小インクルーシブ」として、実践していこうと思います。具体的なプランについては、次回。
防災
静岡県立沼津商業高校(駿東郡清水町徳倉)では、18日午後3時ごろ北側の裏山が高さ10数メートルにわたって崩れ、一部が校舎脇に流れ込んでいるのが見つかったそうです。夕方のニュースで観て、びっくりしました。
他人事ではないので、グーグルマップで、学校周辺の地形を確認してみました。
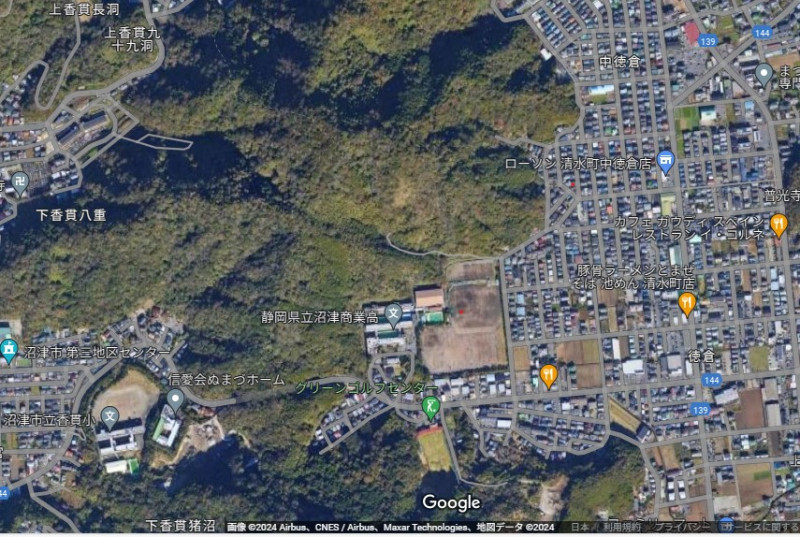
ハザードマップでも、土砂災害警戒区域になっているのが分かりました。
300347794.pdf (town.shimizu.shizuoka.jp)
本校でも、大雨のときの対応を校長、教頭、教務主任と改めて協議しました。土砂災害の危険性がかなり高まったときは、以下のような動きを想定しました。
① 笠原コミュニティーセンターで通行止めとして、正門からの出入りを止める。
② 西門の坂に職員が付き、児童が安全に通行できるように見届ける。坂に大量の水が流れこみ、歩行の妨げになるときは、西門も通行止めとし、東門からの出入りのみとする。
③ 倒木、土砂崩れ、地割れなどを発見したときは、学校教育課と協議の上、休校とする。
授業
6年生が、分数のわり算の学習をしています。小数のわり算は、筆算で解いてもけっこう面倒くさいのですが、分数のわり算は筆算しなくても解けます。分数とわり算は、相性がよいのです。
それは、分数がわり算だからです。わり算の記号を思い出してください。÷の・を数字に置きかえれば分数になります。
12÷3の答えは、3ぶんの12です。整数に直して4になります。どんなにむずかしいわり算でも、商を分数で表してよいのであれば簡単です。例えば4872÷56の商は、56ぶんの4872で間違いではありません。商を整数で表すと87になるのです。
わり算の筆算をするのは、小学校のときだけと前回書きました。中学校や高等学校では、わり算は分数で表すようになります。中学校の数学でわり算の筆算に苦しめられることはないので安心してください。でも、今のうちにわり算の筆算を身に付けておかないと、大人になっても解けません。小学校の算数は、小学校のうちに身に付けておきましょう。
パソコンのキーボードを見てください。「÷」のキーがありませんね。それは、世界のほとんどの国では、「÷」ではなく「/」や「:」が使われているからです。もしかしたら、未来の算数の教科書では、「÷」の記号は使われなくなっているかもしれません。
防災
授業
わり算の正体は、ひき算です。だから、ひき算におきかえれば、2年生でも解けます。例えば、9÷3ですが、9から3を引いていくと、何回引けるかということをきいているのです。
1回目 9-3=6
2回目 6-3=3
3回目 3-3=0
もう引けません。3回引けたので9÷3=3なのです。
10÷2は、10-2-2-2-2-2=0で5回引けたので、答えは5です。
わり算はひき算だと知っていると、小数のわり算で商が、割られる数よりも大きくなっても驚きません。例えば、1÷0.2の場合、商は1よりも大きくなります。わり算をすると小さくなると思い込むと、混乱してしまうのです。しかし、ひき算に置き換えて考えれば、1-0.2-0.2-0.2-0.2ー0.2=0で5回引けるから、商は5だと分かります。
数が大きくなると、ひき算の回数が多くなるので、筆算で解く方が簡単なだけなのです。108÷9を筆算で解くということは、1回ずつ引くのは面倒なので、まとめて10回先に引いておいて、残りをひき算にすることです。つまり、
10回分のひき算 108-90=18
残りのひき算2回分 18-9-9=0
10+2で、全部で12回引いたから、商は12。
テストで、わり算が分からなかったとき、ひき算にして答えを出すのもアリだと思います。確かめに使ってもよいです。
でも、わり算の筆算は、小学生でしか使いません。中学生になると、わり算自体がなくなります。そのかわり・・・